ФИЛИПЕНКО ГЕННАДИЙ ГРИГОРЬЕВИЧ
Пенсионер,
Гродненский филиал Казанского научно-исследовательского
радиотехнологического института 1986-1992
ПРИРОДА МЕТАЛЛИЧЕСКОЙ СВЯЗИ И ПОПРАВЛЕННАЯ ТАБЛИЦА ЭЛЕМЕНТОВ.
Аннотация:
Обычно в литературе металлическая связь описывается, как осуществленная
посредством обобществления внешних электронов атомов и не обладающая свойством
направленности. Хотя встречаются попытки (см. ниже) объяснения направленной металлической
связи т.к. элементы кристаллизуются в определенный тип решетки.
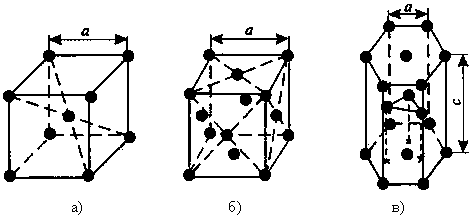
Рис.1. Основные типы кристаллических решеток:
а – объемно-центрированная кубическая; б – гранецентрированная кубическая; в – гексагональная плотноупакованная.
В работе \"К вопросу о металлической связи в плотнейших упаковках химических элементов\"
показано, что металлическая связь в плотнейших упаковках (ГЕК и ГЦК) между цент-
ральноизбранным атомом и его соседями в общем случае, предположительно,
осуществляется посредством 9 (девяти) направленных связей, в отличие от числа соседей равного
12 (двенадцати) (координационное число).
Наверное \"чужие\" 3 (три) атома присутствуют в координационном числе 12 стереометрически,
а не по причине связи.
Ответ должна дать экспериментальная проверка.
FILIPENKA HENADZI
Pensioner, Grodno branch of the Kazan Research Radio Technology Institute 1986-1992
THE NATURE OF METALLIC CONNECTION.
Abstract:
Usually in the literature the metal bond is described as being realized by means of the
socialization of the outer electrons of atoms and not possessing the directional property. Although there
are attempts (see below) for an explanation of the directional metallic connecti
on. the elements crystallize into a specific type of lattice.
In the work "On the question of the metal bond in the densest packets of chemical elements" it was
shown that in the general case, the metal bond in the closest packings (HEC and fcc) between the
centrally chosen atom and its neighbors is presumably carried out by means of nine (nine) directiona l
bonds, in contrast to the number of neighbors equal to 12 (twelve) (coordination number).
Probably \"strange \" 3 (three) atoms are present in the coordination number 12 stereometrically, and
not because of the connection. htp://natureofcrystalstructure.blogspot.com
The answer should be an experimental test.
В литературе приводится много факторов влияющих на кристаллизацию
поэтому решил их максимально убрать, и модель металла в статье скажем так
идеальная, т.е. все атомы одинаковые (чистый металл) без включений без
внедрений, без дефектов и т.д. используя эффект Холла и другие данные по
свойствам а также рассчеты Ашкрофта и Мермина , у меня главным определяющим
тип решетки фактором оказался остов атома или ион, который получился в
результате передачи части электронов в зону проводимости.
Оказалось, что металлическая связь обусловлена не только обобществлением
электронов, а и внешними электронами атомных остовов, которые определяют
направленность или тип кристаллической решетки.
Изменение типа решетки металла может быть связано с переходом электрона
в зону проводимости или возвратом его из этой зоны. Фазовый переход.
Основная проблема состоит в том, что используя рентген определили
кристаллические решетки разных материалов,а почему они такие, а не другие пока
не известно. Например медь кристаллизуется в ГЦК решетку, а железо в ОЦК,
которая при нагреве становиться ГЦК и этот переход используется при термообработке
сталей. Медь при нагреве кристаллическую решетку не изменяет.
Введение
Пока невозможно в общем случае вывести из квантовомеханических расчетов кри-
сталлическую структуру металла по электронному строению атома,
хотя, например, Ганцхорн и Делингер указали на возможную связь между
наличием кубической объемно-центрированной решетки в подгруппах титана,
ванадия, хрома и наличием в атомах этих металлов валентных d-орбиталей.
Нетрудно заметить, что четыре гибридные орбитали направлены по четырем
телесным диагоналям куба и хорошо приспособлены для связи каждого атома с его
8 соседями в кубической объемноцентрированной решетке. При этом оставшиеся
орбитали направлены к центрам граней элементарной ячейки и, возможно, могут
принимать участие в связи атома с шестью его вторыми соседями /3/ стp. 99.
Первое координационное число (К.Ч.1) \"8\" плюс второе координационное число (К.Ч.2)
\"6\" в сумме равно \"14\".
Попытаемся связать внешние электроны атома данного элемента со
структурой его кристаллической решетки, учитывая необходимость направленных
связей (химия) и наличие обобществленных электронов (физика), ответственных за
гальваномагнитные свойства.
Согласно /1/ стр.20, число Z-электроны в зоне проводимости, получено
авторами, предположительно, исходя из валентности металла по кислороду,
водороду и обязано быть подвергнуто сомнению, т.к. экспериментальные данные
по Холлу и модулю всестороннего сжатия близки к теоретическим только для
щелочных металлов. ОЦК решетка, Z=1 не вызывает сомнений. Координационное
число равно 8.
На простых примерах покажем, что на одну связь у алмаза при плотности
упаковки 34% и координационном числе 4 приходится 34%:4=8,5%.

У кубической примитивной решетки плотность упаковки 52% и
координационное число 6 приходится 52%:б=8,66%.
У кубической объемноцентрированной решетки плотность упаковки 68% и
координационное число 8 приходится 68%:8=8,5%.
У кубической гранецентрированной решетки плотность упаковки 74% и координаци-
онное число 12 приходится 74%:12=6.16% (!!!), а если 74%:9=8,22%.
У гексагональной решетки плотность упаковки 74% и координационное
число 12 приходится 74%:12=6,16%, а если 74%:9=8,22%.(!!!)
Очевидно, что эти 8,66-8,22% несут в себе некий физический смысл.
Оставшиеся 26% кратны 8,66 и 100% гипотетическая плотность упаковки
возможна при наличии 12 связей. Но реальна ли такая возможность?
Внешние электроны последней оболочки или подоболочек атома металла
образуют зону проводимости. Число электронов в зоне проводимости влияет на
постоянную Холла, коэффициент всестороннего сжатия и т.д.
Построим модель металла-элемента так, чтобы оставшиеся, после
заполнения зоны проводимости, внешние электроны последней оболочки или
подоболочек атомного остова неким образом влияли на строение кристаллической
структуры (например: для ОЦК решетки-8 \"валентных\" электронов, а для ГЕК и
ГЦК -12 или 9).
Очевидно, что для подтверждения нашей модели необходимо сравнить
экспериментальные и теоретические данные по Холлу, коэффициенту
всестороннего сжатия и т.д.
ГРУБОЕ, КАЧЕСТВЕННОЕ ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА
ЭЛЕКТРОНОВ В ЗОНЕ ПРОВОДИМОСТИ МЕТАЛЛА-ЭЛЕМЕНТА.
ОБЪЯСНЕНИЕ ФАКТОРОВ, ВЛИЯЮЩИХ НА ОБРАЗОВАНИЕ ТИПА
РЕШЕТКИ МОНОКРИСТАЛЛА И НА ЗНАК ПОСТОЯННОЙ ХОЛ
ЛА.(Алгоритм построения модели)
Измерения поля Холла позволяют определить знак носителей заряда в зоне
проводимости. Одна из замечательных особенностей эффекта Холла заключается,
однако, в том, что в некоторых металлах коэффициент Холла положителен, и
поэтому носители в них должны, видимо, иметь заряд, противоположный заряду
электрона /1/. При комнатной температуре это относится к следующим металлам:
ванадий, хром, марганец, железо, кобальт, цинк, цирконий, ниобий, молибден,
рутений, родий, кадмий, церий, празеодим, неодим, иттербий, гафний, тантал,
вольфрам, рений, иридий, таллий, свинец /2/. Решение этой загадки должна дать
полная квантовомеханическая теория твердого тела.
Примерно, как для некоторых случаев применения граничных условий
Борна-Кармана, рассмотрим сильно упрощенный случай зоны проводимости.
Вариант первый: тонкая замкнутая трубка, полностью заполненная
электронами кроме одного. Диаметр электрона примерно равен диаметру трубки.
При таком заполнении зоны, при локальном передвижении электрона, наблюдается
противоположное движение \"места\" незаполнившего трубку, электрона, то есть
движение неотрицательного заряда. Вариант второй: в трубке один электрон -
возможно движение только одного заряда -отрицательно заряженного электрона.
Из этих двух крайних вариантов видно, что знак носителей, определяемых по
коэффициенту Холла, в какой-то степени, должен зависеть от наполнения зоны
проводимости электронами. Рисунок 1.

Рис. 1. Схематическое изображение зоны проводимости двух разных металл
ов. (Масштабы не соблюдены).
а) -вариант первый;
б) -вариант второй.
На порядок движения электронов также будут накладывать свои условия и
структура зоны проводимости, и температура, и примеси, дефекты, а для
магнитных материалов и рассеяние на магнитных квазичастицах -магнонах.
В приведенной ниже таблице нетрудно заметить, что почти все металлы-
сверхпроводники в зоне проводимости содержат по два и более электронов от
атома. Это металлы: цирконий, цинк, вольфрам, ванадий, таллий, титан, тантал,
рутений, рений, свинец, осмий, ниобий, лантан, иридий, гафний, кадмий,
алюминий.
Так как рассуждения наши грубые, учитываем в дальнейшем пока только
наполнение зоны проводимости электронами. Заполним зону проводимости
электронами так, чтобы внешние электроны атомных остовов оказывали влияние
на образование типа кристаллизационной решетки. Предположим, что число
внешних электронов на последней оболочке атомного остова, после заполнения
зоны проводимости, равно числу атомов соседей (координационному числу) /5/.
Координационные числа ГЕК, ГЦК (гексагональной и гранецентрированной)
плотнейших упаковок 12(9) и 18, а объемноцентрированной решетки (ОЦК)8и14/3/.
Построим таблицу с учетом вышеизложенного. Температура комнатная.
| Element | RH . 1010 (м3/K) | Z. (number) | Z kernel (number) | Lattice type |
| Na | -2,30 | 1 | 8 | body-centered |
| Mg | -0,90 | 1 | 9 | volume-centered |
| Al | -0,38 | 2 | 9 | face-centered |
| Al | -0,38 | 1 | 12 | face-centered |
| K | -4,20 | 1 | 8 | body-centered |
| Ca | -1,78 | 1 | 9 | face-centered |
| Ca | T=737K | 2 | 8 | body-centered |
| Sc | -0,67 | 2 | 9 | volume-centered |
| Sc | -0,67 | 1 | 18 | volume-centered |
| Ti | -2,40 | 1 | 9 | volume-centered |
| Ti | -2,40 | 3 | 9 | volume-centered |
| Ti | T=1158K | 4 | 8 | body-centered |
| V | +0,76 | 5 | 8 | body-centered |
| Cr | +3,63 | 6 | 8 | body-centered |
| Fe | +8,00 | 8 | 8 | body-centered |
| Fe | +8,00 | 2 | 14 | body-centered |
| Fe | Т=1189K | 7 | 9 | face-centered |
| Fe | Т=1189K | 4 | 12 | face-centered |
| Co | +3,60 | 8 | 9 | volume-centered |
| Co | +3,60 | 5 | 12 | volume-centered |
| Ni | -0,60 | 1 | 9 | face-centered |
| Cu | -0,52 | 1 | 18 | face-centered |
| Cu | -0,52 | 2 | 9 | face-centered |
| Zn | +0,90 | 2 | 18 | volume-centered |
| Zn | +0,90 | 3 | 9 | volume-centered |
| Rb | -5,90 | 1 | 8 | body-centered |
| Y | -1,25 | 2 | 9 | volume-centered |
| Zr | +0,21 | 3 | 9 | volume-centered |
| Zr | Т=1135К | 4 | 8 | body-centered |
| Nb | +0,72 | 5 | 8 | body-centered |
| Mo | +1,91 | 6 | 8 | body-centered |
| Ru | +22 | 7 | 9 | volume-centered |
| Rh | +0,48 | 5 | 12 | face-centered |
| Rh | +0,48 | 8 | 9 | face-centered |
| Pd | -6,80 | 1 | 9 | face-centered |
| Ag | -0,90 | 1 | 18 | face-centered |
| Ag | -0,90 | 2 | 9 | face-centered |
| Cd | +0,67 | 2 | 18 | volume-centered |
| Cd | +0,67 | 3 | 9 | volume-centered |
| Cs | -7,80 | 1 | 8 | body-centered |
| La | -0,80 | 2 | 9 | volume-centered |
| Ce | +1,92 | 3 | 9 | face-centered |
| Ce | +1,92 | 1 | 9 | face-centered |
| Pr | +0,71 | 4 | 9 | volume-centered |
| Pr | +0,71 | 1 | 9 | volume-centered |
| Nd | +0,97 | 5 | 9 | volume-centered |
| Nd | +0,97 | 1 | 9 | volume-centered |
| Gd | -0,95 | 2 | 9 | volume-centered |
| Gd | T=1533K | 3 | 8 | body-centered |
| Tb | -4,30 | 1 | 9 | volume-centered |
| Tb | Т=1560К | 2 | 8 | body-centered |
| Dy | -2,70 | 1 | 9 | volume-centered |
| Dy | Т=1657К | 2 | 8 | body-centered |
| Er | -0,341 | 1 | 9 | volume-centered |
| Tu | -1,80 | 1 | 9 | volume-centered |
| Yb | +3,77 | 3 | 9 | face-centered |
| Yb | +3,77 | 1 | 9 | face-centered |
| Lu | -0,535 | 2 | 9 | volume-centered |
| Hf | +0,43 | 3 | 9 | volume-centered |
| Hf | Т=2050К | 4 | 8 | body-centered |
| Ta | +0,98 | 5 | 8 | body-centered |
| W | +0,856 | 6 | 8 | body-centered |
| Re | +3,15 | 6 | 9 | volume-centered |
| Os | <0 | 4 | 12 | volume-centered |
| Ir | +3,18 | 5 | 12 | face-centered |
| Pt | -0,194 | 1 | 9 | face-centered |
| Au | -0,69 | 1 | 18 | face-centered |
| Au | -0,69 | 2 | 9 | face-centered |
| Tl | +0,24 | 3 | 18 | volume-centered |
| Tl | +0,24 | 4 | 9 | volume-centered |
| Pb | +0,09 | 4 | 18 | face-centered |
| Pb | +0,09 | 5 | 9 | face-centered |
Где Rh- коэффициент Холла.
Z -предполагаемое число электронов, отданное одним атомом в зону проводимости
Z остов. -число внешних электронов атомного остова на последней оболочке.
Тип решетки -тип кристаллической структуры металла при комнатной
температуре и в некоторых случаях для температур фазовых переходов (T).
Выводы.
Несмотря на грубые допущения, из таблицы видно, что, чем больше атом
элемента отдает электронов в зону проводимости, тем положительнее постоянная
Холла, и, наоборот, постоянная Холла отрицательна для элементов, отдавших в
зону проводимости один-два электрона, что не противоречит выводам Пайерлса , а
также просматривается связь между электронами проводимости (Z) и валентными
электронами (Zостов), обуславливающими кристаллическую структуру.
Фазовые переходы элемента из одной решетки в другую можно объяснить
перебросом в зону проводимости металла одного из внешних электронов атомного
остова или его возвратом из зоны проводимости на внешнюю оболочку остова под
воздействием внешних факторов (давление, температура) .
Пытались дать разгадку, а получили новую, довольно хорошо объясняющую
физико-химические свойства элементов, загадку-это \"координационное число\" -
9 (девять) для ГЦК и ГЕК. Такое частое явление числа-9 в приведенной таблице
наводит на мысль, что плотнейшие упаковки недостаточно исследованы.
Чтобы не загромождать таблицу, пропущены
варианты возможных связей атомов, например никеля и меди, с атомами из второй координационной сферы 9+6=15 и у никеля один электрон проводимости, а у меди два.
Чтобы не загромождать таблицу, пропущены
варианты возможных связей атомов, например никеля и меди, с атомами из второй координационной сферы 9+6=15 и у никеля один электрон проводимости, а у меди два.
Методом обратного отсчета от экспериментальных значений коэффициента всесто-
роннего сжатия к теоретическим по формулам Ашкрофта и Мермина /1/,
определяя число Z, для некоторых элементов, можно убедиться о его близком совпадении с приведенным в таблице 1.
Металлическая связь представляется обусловленной: как обобществленными элек-
тронами, так и \"валентными\" -внешними электронами атомного остова.
Литература:
1. Н.Ашкрофт, Н.Мермин \"Физика твердого тела\". Москва, 1979г
2. Г.В.Самсонов \"Справочник \"Свойства элементов\".Москва,1976г.
3. Г.Кребс \"Основы кристаллохимии неорганических соединений\". Москва, l971r.
4. Я.Г.Дорфман, И.К.Кикоин \"Физика металлов\". Ленинград, 1933г.
5. Г.Г.Скидельский \"От чего зависят свойства кристаллов\". \"Инженер\" No 8, 1989г.
6. Г.Г.Филипенко "Природа кристаллических структур" http://structurecrystal.blogspot.com
ПРИЛОЖЕНИЕ 1.
Металлическая связь в плотнейших упаковках (ГЕК, ГЦК).
Из рассуждений о числе направленных связей (или псевдосвязей, т.к. между
соседними атомами металла находится зона проводимости) равном девяти по числу
внешних электронов атомного остова для плотнейших упаковок, вытекает, что по
аналогии с решеткой ОЦК (восемь атомов-соседей в первой координационной
сфере) у ГЕК и ГЦК решеток в первой координационной сфере, должно быть
девять, а имеем 12 атомов. Но 9 атомов соседей, связанных любым
центральноизбранным атомом, косвенно подтверждаются экспериментальными
данными по Холлу и модулю всестороннего сжатия (да и в опытах по эффекту де
Гааза-ван -Альфена число осцилляций кратно девяти).
На рис.1.1, d, е, показаны координационные сферы в плотнейших
гексагональной и кубической упаковках.

Рис. 1.1. Плотные упаковки
Обратим внимание, что в гексагональной упаковке треугольники верхнего и
нижнего оснований повернуты в одну и ту же сторону, а в кубической -в разные.
Литература:
Б.Ф.Ормонт \"Введение в физическую химию и кристаллохимию полупроводников\",
Москва, 1968 год.
ПРИЛОЖЕНИЕ 2.
Теоретический расчет модуля всесторонне
го сжатия (В).
В=(6,13/(rs/а0))5*1010 дн/см2,
где В -модуль всестороннего сжатия, а0 -боровский радиус, rs -
радиус сферы, объем которой равен объему, приходящемуся на один электрон проводимости.
rs=(3/4np)1/3 , p=3,14
где
n-плотность электронов проводимости.
1. Расчеты по Ашкрофту и Мермину.
Table 1. Calculation according to Ashcroft and Mermine Element Z rs/ao theoretical calculated
Table 2. Calculation according to the models considered in this paper. (Филипенко Г.Г.)
| Z | rs/a0 | B theoretical | B calculated | |
| Cs | 1 | 5.62 | 1.54 | 1.43 |
| Cu | 1 | 2.67 | 63.8 | 134.3 |
| Ag | 1 | 3.02 | 34.5 | 99.9 |
| Al | 3 | 2.07 | 228 | 76.0 |
| Z | rs/a0 | B theoretical | B calculated | |
| Cs | 1 | 5.62 | 1.54 | 1.43 |
| Cu | 2 | 2.12 | 202.3 | 134.3 |
| Ag | 2 | 2.39 | 111.0 | 99.9 |
| Al | 2 | 2.40 | 108.6 | 76.0 |
Конечно, давление газов свободных электронов само по себе, одно, не
полностью определяет сопротивление металла сжатию, тем не менее во втором
случае расчета теоретический модуль всестороннего сжатия лежит ближе к
экспериментальному, причем с одной стороны. Очевидно необходим учет второго
фактора -влияние на модуль \"валентных\" или внешних электронов атомного
остова, определяющих кристаллическую решетку.
Эти теоретические исследования металлической связи в чистых однородных металлах
привели меня к тому, что изменения кристаллических решеток лития и бериллия в зависи-
мости от температуры оказались примерно такими же как у скандия и титана соответственно
и задумался о правильности таблицы элементов.
Филипенко Геннадий Григорьевич
ТАБЛИЦА ЭЛЕМЕНТОВ СОГЛАСНО ЗАРЯДОВ ЯДЕР АТОМОВ
TABLE OF ELEMENTS ACCORDING TO CHARGES OF THE NUCLEAR OF ATOMS.
Аннотация:
В данной статье изложены взгляды на классификацию всех известных
химических элементов, тех фундаментальных компонентов, из которых состоит Земля и вся
Вселенная.
Новаторство данной работы состоит в том, что в таблице элементов, построенной согласно
закона Менделеева и правила Ван-ден-Брука, предположительно выявлены новые химические
элементы с атомными номерами 72-75 и 108-111, а также показано, что у тяжелых элементов,
начиная с гафния ядра атомов содержат большее число протонов, чем общепринято.
Разработана модель модель ядра атома, поясняющая соотношение числа протонов к числу нейтронов.
Все ячейки таблицы заполнены. Если эта таблица состоится, то хотелось бы назвать группы
элементов с номерами 72-75 и 108-111, островками Филипенко Г.Г.
Abstract:
In this article, views on the classification of all known chemical elements, those
fundamental components that make up the Earth and the entire universe are set forth.
The innovation of this work is that in the table of elements constructed according
to the Mendeleyev's law and Van Dun Brook's rule, new chemical elements with atomic numbers 72-75 and
108-111 are supposedly revealed, and also it is shown that for heavy elements starting with hafnium,
the nuclei of atoms contain a larger number of protons than is generally accepted.
All cells in the table are full. If this table takes place, I would like to name groups of elements with
the numbers 72-75 and 108-111, the islets of Filipenka Henadzi.
Ключевые слова:
Протон, нейтрон, ядро, атом, элемент, таблица.
Keywords:
proton, neutron, nucleus, atom, element, table.
О таблице элементов и металлической связи в монокристаллах.
Наверное Джеймс Чедвик сделал ошибку, измеряя заряды ядер атомов.
Точнее не ошибку в измерениях, а в том что согласился с таблицей Менделеева и полученный
результат для платины 77,6 был трактован, как заряд ядра равный 78, согласно таблице.
Для меди был получен результат 29,3-больше истинного на 0,3, для серебра 46,3 уже меньше
истинного на 0,7, а для платины меньше “истинного” всего на 0,6. Уменьшение связано с
экранированием протонов друг другом при измерениях. Поэтому для платины с зарядом 78 результат
должен был быть меньше полученного, или другими словами у атома платины заряд ядра больше 78
и равен 82.
Построим модель ядра атома. Знаем что в ядре находятся протоны и нейтроны. В каждом
последующем элементе на протон больше, а нейтронов на несколько. Почему? Обьем растет быстрее
чем поверхность. При альфа излучении из ядра вылетают ядра гелия примерно одинаковых энергий.
Разместив ядра гелия в поверхностном слое ядра атома, получаем с некоторой точностью, что остальные
нейтроны находятся внутри ядра. И вопрос а может ли и когда находится внутри ядра протон.
Согласно закона Менделеева и правила Брука, а также полученной модели ядра разработана
физическая таблица элементов- http://physicaltable.blogspot.com
таблица элементов
| H 1 | He 2 | Li 3 | Be 4 | B 5 | C 6 | N 7 | O 8 | F 9 | Ne 10 | Na 11 | Mg 12 | Al 13 | Si 14 | P1 5 | S 16 | Cl 17 | A 1 | |
| K 19 | Ca 20 | Sc 21 | Ti 22 | V 23 | Cr 24 | Mn 25 | Fe 26 | Co 27 | Ni 28 | Cu 29 | Zn 30 | Ga 31 | Ge 32 | As 33 | Se 34 | Br 35 | Kr 36 | |
| Rb 37 | Sr 38 | Y 39 | Zr 40 | Nb 41 | Mo 42 | Tc 43 | Ru 44 | Rh 45 | Pd 46 | Ag 47 | Cd 48 | In 49 | Sn 50 | Sb 51 | Te 52 | I 53 | Xe 54 | |
| Cs 55 | Ba 56 | La 57 | Ce 58 | Pr 59 | Nd 60 | Pm 61 | Sm 62 | Eu 63 | Gd 64 | Tb 65 | Dy 66 | Ho 67 | Er 68 | Tu 69 | Yb 70 | Lu 71 | ? 72 | |
| ? 73 | ? 74 | ? 75 | Hf 76 | Ta 77 | W 78 | Re 79 | Os 80 | Ir 81 | Pt 82 | Au 83 | Hg 84 | Tl 85 | Pb 86 | Bi 87 | Po 88 | At 89 | Rn 90 | |
| Fr 91 | Ra 92 | Ac 93 | Th 94 | Pa 95 | U 96 | Np 97 | Pu 98 | Am 99 | Cm 100 | Bk 101 | Cf 102 | Es 103 | Fm 104 | Md 105 | No 106 | Lr 107 | ? | |
Таблица 2.
Физическая таблица элементов.
В этой таблице платина находится под номером 82. Протоны начинают размещаться внутри
ядра с 72 по 75 элемент. Пока не открытые элементы.
В таблице заполнены все ячейки. У Д.И.Менделеева не таблица, а сложная химическая
конструкция. Лантаноиды и актиноиды, которые должны располагаться вертикально согласно их
химических свойств, по “домашнему” расположены под таблицей горизонтально. Периодический
закон входит не только в химию, но и в физику.
Прошу повторить опыт джеймса чедвика по измерению заряда ядра атома платины. Заряды
ядер меди и серебра сомнению не подлежат. Но согласно этой таблице элементов построенной как по
закону Менделеева а также по правилу ван-Брука начиная с гафния заряды ядер могут быть на 4
единицы больше чем принято на сегодня при той же массе. Для задания режимов на АЭС, наверное
важно знать истинный заряд ядра урана.
Дмитрий Иванович интуитивно чувствовал, что должна быть таблица элементов, а не сложная
конструкция, как у него, но ему наверное не хватило знаний по устройству атома и ядра атома.
Поэтому лантаноиды и актиноиды у него расположены горизонтально.
Правило Ван-ден-Брука, любителя ядерной физики, оказалось более общим, чем
периодичность Менделеева и расчеты квантовой механики. У таблицы должны быть заполнены все
ячейки согласно закона или правила, а при незаполнении какой-то, должно быть обьяснение этого
этим законом или правилом. Поэтому ячейки физической таблицы были заполнены как
в http://physicaltable.blogspot.com и появились неизвестные элементы с номерами 72-75 и 108-111.
Которые требовали обьяснения. При рассмотрении результатов измерения зарядов ядер или
атомных номеров Джеймсом Чедвиком, я заметил, что заряд ядра платины скорее равен не 78, а
стремится к 82, что соответствует разработанной таблице. Почти 30 лет поднимаю вопрос о
повторении измерений зарядов ядер атомов, т.к. у урана, наверное, заряд больше, чем принято, а он
применяется на АЭС.
Литий и бериллий в зависимости от температуры изменяют кристаллические решетки
примерно также как скандий и титан. Что говорит о правильности нашей таблицы химических
элементов.
Библиографический список:
1. Г. Г. Филипенко. «Подозрительные» области в
периодической системе, "Техника и наука", No4,
Москва, 1990.
2. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", No4, Москва, 1991.
3. Доклады независимых авторов 2005 выпуск 1, стр 172-183.
4.Физическая таблица элементов. http://physicaltable.blogspot.com
Эта работа на английском языке.
Abstract.
The
main problem is that using X-rays, we have determined the crystal
lattices of different materials, and why they are so, and not others are
not yet known. For
example, copper crystallizes in the fcc lattice, and iron in the bcc,
which becomes fcc on heating, this is used for heat treatment of steels.
Copper does not change the crystal lattice when heated.

Рис.1. Основные типы кристаллических решеток:
а – объемно-центрированная кубическая; б – гранецентрированная кубическая; в – гексагональная плотноупакованная. (in Russian)
There are many factors affecting the crystallization in the literature, so they decided to remove them as much as possible, and the metal model in the article, say so, is ideal, i.e. all atoms are the same (pure metal) without inclusions, without implants, without defects, etc. using the Hall effect and other data on properties, as well as the calculations of Ashcroft and Mermin, my main determining factor for the type of lattice was the core of the atom or ion, which resulted from the transfer of some electrons to the conduction band.
It turned out that the metal bond is due not only to the socialization of electrons, but also to external electrons of atomic cores, which determine the direction or type of the crystal lattice.
The change in the type of metal lattice can be connected with the transition of an electron to the conduction band or its return from this zone. Phase transition.
It
is shown that in the general case, the metal bond in the closest
packages (hec and fcc) between the centrally chosen atom and its
neighbors is presumably carried out by means of nine (9) directional
bonds, in contrast to the number of neighbors equal to 12 (twelve)
(coordination number) .
Probably the "alien" 3 (three) atoms are present in the coordination number 12 stereometrically, and not because of the connection. The answer is to give an experimental test.
Probably the "alien" 3 (three) atoms are present in the coordination number 12 stereometrically, and not because of the connection. The answer is to give an experimental test.
Introduction
While it is not possible in general to derive from the quantum mechanical calculations the crystal structure of the metal over the electronic structure of the atom, although, for example, Gantshorn and Delinger pointed out a possible relationship between the presence of a cubic body-centered lattice in the subgroups of titanium, vanadium, chromium and the presence of valence d - orbitals. It is easy to see that four hybrid orbitals are directed along four solid cube diagonals and are well suited for coupling each atom to its 8 neighbors in a cubic body-centered lattice. In this case, the remaining orbitals are directed to the centers of the faces of the unit cell and, possibly, can participate in the connection of the atom with its six second neighbors / 3 /.
The first coordination number (K.Ch.1) "8" plus the second coordination number (K.C.2) "6" is equal to "14".
In simple examples, we show that one bond for a diamond at a packing density of 34% and a coordination number of 4 is 34%: 4 = 8.5%.
While it is not possible in general to derive from the quantum mechanical calculations the crystal structure of the metal over the electronic structure of the atom, although, for example, Gantshorn and Delinger pointed out a possible relationship between the presence of a cubic body-centered lattice in the subgroups of titanium, vanadium, chromium and the presence of valence d - orbitals. It is easy to see that four hybrid orbitals are directed along four solid cube diagonals and are well suited for coupling each atom to its 8 neighbors in a cubic body-centered lattice. In this case, the remaining orbitals are directed to the centers of the faces of the unit cell and, possibly, can participate in the connection of the atom with its six second neighbors / 3 /.
The first coordination number (K.Ch.1) "8" plus the second coordination number (K.C.2) "6" is equal to "14".
In simple examples, we show that one bond for a diamond at a packing density of 34% and a coordination number of 4 is 34%: 4 = 8.5%.

In a cubic primitive lattice, the packing density is 52% and the coordination number 6 is 52%: b = 8.66%.
In a cubic body-centered lattice, the packing density of 68% and the coordination number 8 are 68%: 8 = 8.5%.
In a face-centered cubic lattice, the packing density is 74% and the coordination number 12 is 74%: 12 = 6.16%, and if 74%: 9 = 8.22%.
In a hexagonal lattice, the packing density is 74% and the coordination number 12 is 74%: 12 = 6.16%, and if 74%: 9 = 8.22%.
Obviously, these 8.66-8.22% carry a certain physical meaning. The remaining 26% is a multiple of 8.66 and 100% hypothetical packing density is possible with 12 links. But is this possibility real?
The outer electrons of the last shell or subshells of the metal atom form a conduction band. The number of electrons in the conduction band affects the Hall constant, the coefficient of all-round compression, and so on.
Let us construct the model of the metal element so that the remaining electrons, after filling the conduction band, the external electrons of the last shell or subshells of the atomic core somehow influenced the structure of the crystal structure (for example: for bcc lattice-8 valence electrons, and for HEC and FCC -12 or 9).
Obviously, to confirm our model it is necessary to compare the experimental and theoretical data on Hall, the coefficient of all-round compression, and so on.
GROSS, QUALITATIVE DETERMINATION OF QUANTITY
ELECTRONS IN THE CONDUCTIVITY METAL - ELEMENT.
EXPLANATION OF FACTORS INFLUENCING THE EDUCATION OF TYPE
GRANTS OF THE MONOCRYSTAL AND ON THE SIGN OF THE CONSTANT HALL.
(Algorithm for constructing a model)
ELECTRONS IN THE CONDUCTIVITY METAL - ELEMENT.
EXPLANATION OF FACTORS INFLUENCING THE EDUCATION OF TYPE
GRANTS OF THE MONOCRYSTAL AND ON THE SIGN OF THE CONSTANT HALL.
(Algorithm for constructing a model)
Let us try to relate the external electrons of the atom of a given
element to the structure of its crystal lattice, taking into account the
need for directed bonds (chemistry) and the presence of socialized
electrons (physics) responsible for galvanomagnetic properties.
Measurements of the Hall field make it possible to determine the sign of the charge carriers in the conduction band. One
of the remarkable features of the Hall effect is, however, that in some
metals the Hall coefficient is positive, and therefore the carriers in
them must apparently have a charge opposite to the electron charge / 1
/. At
room temperature, this refers to the following metals: vanadium,
chromium, manganese, iron, cobalt, zinc, zirconium, niobium, molybdenum,
ruthenium, rhodium, cadmium, cerium, praseodymium, neodymium,
ytterbium, hafnium, tantalum, tungsten, rhenium, iridium , thallium, lead / 2 /. The solution of this puzzle should be given by a complete quantum mechanical theory of a solid.
Approximately, as for some cases of application of the Born-Karman boundary conditions, we consider a strongly simplified one-dimensional case of the conduction band. Option one: a thin closed tube, completely filled with electrons except one. The diameter of the electron is approximately equal to the diameter of the tube. With such a filling of the zone, with the local movement of the electron, there is an opposite movement of the "place" of the non-filled tube, the electron, that is, the motion of a non-negative charge. Option two: in the tube of one electron - it is possible to move only one charge - a negatively charged electron. From these two extreme variants it is seen that the sign of carriers, determined from the Hall coefficient, to some extent, should depend on the filling of the conduction band by electrons. Picture 1.
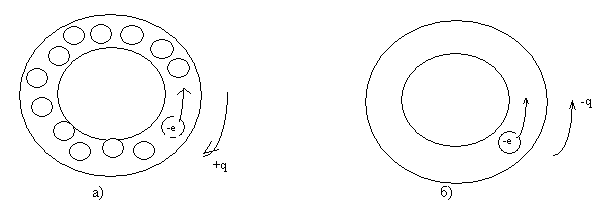
Fig. 1. Schematic representation of the conduction band of two different metals (Scales not observed).
a) - the first option;
b) the second option.
Approximately, as for some cases of application of the Born-Karman boundary conditions, we consider a strongly simplified one-dimensional case of the conduction band. Option one: a thin closed tube, completely filled with electrons except one. The diameter of the electron is approximately equal to the diameter of the tube. With such a filling of the zone, with the local movement of the electron, there is an opposite movement of the "place" of the non-filled tube, the electron, that is, the motion of a non-negative charge. Option two: in the tube of one electron - it is possible to move only one charge - a negatively charged electron. From these two extreme variants it is seen that the sign of carriers, determined from the Hall coefficient, to some extent, should depend on the filling of the conduction band by electrons. Picture 1.

Fig. 1. Schematic representation of the conduction band of two different metals (Scales not observed).
a) - the first option;
b) the second option.
The motion of the electrons will also be imposed by an order of magnitude on the structure of the conduction band, temperature, impurities, and defects, and magnons for magnetic materials and scattering by magnetic quasiparticles.
In the table below it is not difficult to see that almost all the superconductor metals in the conduction band contain two or more electrons from the atom. They are metals: zirconium, zinc, tungsten, vanadium, thallium, titanium, tantalum, ruthenium, rhenium, lead, osmium, niobium, lanthanum, iridium, hafnium, cadmium, aluminum.
Since our arguments are crude, we take into account in the sequel so far only the filling of the conduction band by electrons. We fill the conduction band with electrons so that the outer electrons of the atomic cores exert influence on the formation of the type of crystallization lattice. Suppose that the number of external electrons on the last shell of the atomic core, after filling the conduction band, is equal to the number of neighbors atoms (coordination number) / 5 /. Coordination numbers of HEC, fcc (hexagonal and face-centered) densest packages 12 and 18, and body-centered lattice (bcc) 8 and 14/3 /.
Let's construct the table taking into account the above. The room temperature.
Element RH 1010 (m3 / K) Z. (pcs.) Z frame (pcs.) Grid type
The below table is filled in compliance with the above judgements.
| Element | RH . 1010 (м3/K) | Z. (number) | Z kernel (number) | Lattice type |
| Na | -2,30 | 1 | 8 | body-centered |
| Mg | -0,90 | 1 | 9 | volume-centered |
| Al | -0,38 | 2 | 9 | face-centered |
| Al | -0,38 | 1 | 12 | face-centered |
| K | -4,20 | 1 | 8 | body-centered |
| Ca | -1,78 | 1 | 9 | face-centered |
| Ca | T=737K | 2 | 8 | body-centered |
| Sc | -0,67 | 2 | 9 | volume-centered |
| Sc | -0,67 | 1 | 18 | volume-centered |
| Ti | -2,40 | 1 | 9 | volume-centered |
| Ti | -2,40 | 3 | 9 | volume-centered |
| Ti | T=1158K | 4 | 8 | body-centered |
| V | +0,76 | 5 | 8 | body-centered |
| Cr | +3,63 | 6 | 8 | body-centered |
| Fe | +8,00 | 8 | 8 | body-centered |
| Fe | +8,00 | 2 | 14 | body-centered |
| Fe | Т=1189K | 7 | 9 | face-centered |
| Fe | Т=1189K | 4 | 12 | face-centered |
| Co | +3,60 | 8 | 9 | volume-centered |
| Co | +3,60 | 5 | 12 | volume-centered |
| Ni | -0,60 | 1 | 9 | face-centered |
| Cu | -0,52 | 1 | 18 | face-centered |
| Cu | -0,52 | 2 | 9 | face-centered |
| Zn | +0,90 | 2 | 18 | volume-centered |
| Zn | +0,90 | 3 | 9 | volume-centered |
| Rb | -5,90 | 1 | 8 | body-centered |
| Y | -1,25 | 2 | 9 | volume-centered |
| Zr | +0,21 | 3 | 9 | volume-centered |
| Zr | Т=1135К | 4 | 8 | body-centered |
| Nb | +0,72 | 5 | 8 | body-centered |
| Mo | +1,91 | 6 | 8 | body-centered |
| Ru | +22 | 7 | 9 | volume-centered |
| Rh | +0,48 | 5 | 12 | face-centered |
| Rh | +0,48 | 8 | 9 | face-centered |
| Pd | -6,80 | 1 | 9 | face-centered |
| Ag | -0,90 | 1 | 18 | face-centered |
| Ag | -0,90 | 2 | 9 | face-centered |
| Cd | +0,67 | 2 | 18 | volume-centered |
| Cd | +0,67 | 3 | 9 | volume-centered |
| Cs | -7,80 | 1 | 8 | body-centered |
| La | -0,80 | 2 | 9 | volume-centered |
| Ce | +1,92 | 3 | 9 | face-centered |
| Ce | +1,92 | 1 | 9 | face-centered |
| Pr | +0,71 | 4 | 9 | volume-centered |
| Pr | +0,71 | 1 | 9 | volume-centered |
| Nd | +0,97 | 5 | 9 | volume-centered |
| Nd | +0,97 | 1 | 9 | volume-centered |
| Gd | -0,95 | 2 | 9 | volume-centered |
| Gd | T=1533K | 3 | 8 | body-centered |
| Tb | -4,30 | 1 | 9 | volume-centered |
| Tb | Т=1560К | 2 | 8 | body-centered |
| Dy | -2,70 | 1 | 9 | volume-centered |
| Dy | Т=1657К | 2 | 8 | body-centered |
| Er | -0,341 | 1 | 9 | volume-centered |
| Tu | -1,80 | 1 | 9 | volume-centered |
| Yb | +3,77 | 3 | 9 | face-centered |
| Yb | +3,77 | 1 | 9 | face-centered |
| Lu | -0,535 | 2 | 9 | volume-centered |
| Hf | +0,43 | 3 | 9 | volume-centered |
| Hf | Т=2050К | 4 | 8 | body-centered |
| Ta | +0,98 | 5 | 8 | body-centered |
| W | +0,856 | 6 | 8 | body-centered |
| Re | +3,15 | 6 | 9 | volume-centered |
| Os | <0 | 4 | 12 | volume-centered |
| Ir | +3,18 | 5 | 12 | face-centered |
| Pt | -0,194 | 1 | 9 | face-centered |
| Au | -0,69 | 1 | 18 | face-centered |
| Au | -0,69 | 2 | 9 | face-centered |
| Tl | +0,24 | 3 | 18 | volume-centered |
| Tl | +0,24 | 4 | 9 | volume-centered |
| Pb | +0,09 | 4 | 18 | face-centered |
| Pb | +0,09 | 5 | 9 | face-centered |
Where: RH - Hall constant (Hall coefficient)
Z is the assumed number of electrons, given by one atom to the conduction band
Z skeleton. - number of outer electrons of the atomic core on the last shell.
The lattice type is the type of crystal structure of the metal at room temperature and in some cases for phase transition temperatures (T).
Conclusions.
Despite
the crude assumptions, it can be seen from the table that the larger
the element atom gives electrons to the conduction band, the more
positive the Hall constant, and conversely the Hall constant is negative
for the elements that gave one or two electrons to the conduction band,
which does not contradict the conclusions of Peierls , as
well as the connection between the conduction electrons (Z) and valence
electrons (Zost), which cause the crystal structure.
Using
the method of counting down from the experimental values of the
coefficient of all-round compression to theoretical values using the
formulas of Ashcroft and Mermin [1], determining the number Z, one can
be sure of its close coincidence with that given in Table 1.
The metallic bond appears to be conditioned by both the socialized electrons and the "valence" electrons-the outer electrons of the atomic core.
The metallic bond appears to be conditioned by both the socialized electrons and the "valence" electrons-the outer electrons of the atomic core.
The phase transitions of an element from one lattice to another can be
explained by transferring one of the outer electrons of the atomic core
to the conduction band of the metal or by returning it from the
conduction band to the outer shell of the core under the influence of
external factors (pressure, temperature).
We tried to give a clue, but we got a new, physicochemical properties of the elements, which are pretty well explained, the riddle is a "coordination number" - 9 (nine) for HCC and HEC. Such a frequent occurrence of the number-9 in the table above suggests that the densest packages are not sufficiently investigated.
In order not to clutter up the table, skipped
variants of possible bonds of atoms, for example nickel and copper, with atoms from the second coordination sphere 9 + 6 = 15 and nickel has one conduction electron, and copper has two.
We tried to give a clue, but we got a new, physicochemical properties of the elements, which are pretty well explained, the riddle is a "coordination number" - 9 (nine) for HCC and HEC. Such a frequent occurrence of the number-9 in the table above suggests that the densest packages are not sufficiently investigated.
In order not to clutter up the table, skipped
variants of possible bonds of atoms, for example nickel and copper, with atoms from the second coordination sphere 9 + 6 = 15 and nickel has one conduction electron, and copper has two.
Appendix 1
Metal bond in the closest packages (HEC, HCC)
From the arguments about the number of directed bonds (or pseudo-connections, since there is a conduction band between the neighboring metal atoms), equal to nine in the number of outer electrons of the atomic core for the densest packages, it follows that, by analogy with the bcc lattice (eight neighbor atoms in the first coordination sphere) for HEK and fcc lattices in the first coordination sphere, there should be nine, and we have 12 atoms. But 9 atoms of neighbors bound by any centrally chosen atom are indirectly confirmed by experimental data on the Hall and the modulus of all-round compression (and in the experiments on the de Haas-van Alfene effect, the number of oscillations is a multiple of nine).
Hence, for the three atoms out of 12, we must seek differences from the remaining atoms of the coordination sphere.
From the arguments about the number of directed bonds (or pseudo-connections, since there is a conduction band between the neighboring metal atoms), equal to nine in the number of outer electrons of the atomic core for the densest packages, it follows that, by analogy with the bcc lattice (eight neighbor atoms in the first coordination sphere) for HEK and fcc lattices in the first coordination sphere, there should be nine, and we have 12 atoms. But 9 atoms of neighbors bound by any centrally chosen atom are indirectly confirmed by experimental data on the Hall and the modulus of all-round compression (and in the experiments on the de Haas-van Alfene effect, the number of oscillations is a multiple of nine).
Hence, for the three atoms out of 12, we must seek differences from the remaining atoms of the coordination sphere.
Fig.1.1, d, e shows the coordination spheres in the densest hexagonal and cubic packs.
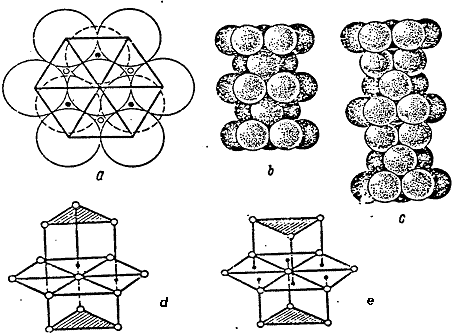
Fig.1.1. Dense Packing.
It should be noted that in the hexagonal packing, the triangles of upper and lower bases are unindirectional, whereas in the hexagonal packing they are not unindirectional.
Fig. 1.1. Tight packing
Let's pay attention, that in a hexagonal packing triangles of the top and bottom bases are turned in one and the same party, and in cubic - in different.
Literature: BF Ormont "Introduction to physical chemistry and crystal chemistry of semiconductors", Moscow, 1968
Let's pay attention, that in a hexagonal packing triangles of the top and bottom bases are turned in one and the same party, and in cubic - in different.
Literature: BF Ormont "Introduction to physical chemistry and crystal chemistry of semiconductors", Moscow, 1968
Appendix 2
Theoretical calculation of the uniform compression modulus (B).
B = (6,13/(rs/ao))5* (10)10 dyne/cm2
Where B is the uniform compression modulus ao is the Bohr radius rs - the radius of the sphere with the volume being equal to
the volume falling at one conductivity electron.
rs=(3/4p n)1/3, p=3,14
Where n is the density of conductivity electrons.
Theoretical calculation of the uniform compression modulus (B).
B = (6,13/(rs/ao))5* (10)10 dyne/cm2
Where B is the uniform compression modulus ao is the Bohr radius rs - the radius of the sphere with the volume being equal to
the volume falling at one conductivity electron.
rs=(3/4p n)1/3, p=3,14
Where n is the density of conductivity electrons.
Table 1. Calculation according to Ashcroft and Mermine Element Z rs/ao theoretical calculated
Table 2. Calculation according to the models considered in this paper
| Z | rs/a0 | B theoretical | B calculated | |
| Cs | 1 | 5.62 | 1.54 | 1.43 |
| Cu | 1 | 2.67 | 63.8 | 134.3 |
| Ag | 1 | 3.02 | 34.5 | 99.9 |
| Al | 3 | 2.07 | 228 | 76.0 |
| Z | rs/a0 | B theoretical | B calculated | |
| Cs | 1 | 5.62 | 1.54 | 1.43 |
| Cu | 2 | 2.12 | 202.3 | 134.3 |
| Ag | 2 | 2.39 | 111.0 | 99.9 |
| Al | 2 | 2.40 | 108.6 | 76.0 |
According
to / 1 /, the number of Z-electrons in the conduction band was obtained
by the authors, presumably based on the valency of the metal over
oxygen and hydrogen, and must be questioned, since the experimental data on Hall and the modulus of all-round compression are close to theoretical only for alkali metals. Bcc grating.
Of
course, the pressure of free-electron gases alone does not completely
determine the resistance of the metal to compression, nevertheless in
the second case of calculation the theoretical modulus of all-round
compression lies closer to the experimental one, on the one hand. Obviously,
it is necessary to take into account the second factor-the effect on
the module of the "valence" or outer electrons of the atomic core, which
determine the crystal lattice.
While still studying at the institute, I tried to explain the phase transitions in barium titanate. Since then I have been working on the nature of crystal lattices and different properties of chemical elements. It
turned out that when heated, the crystal lattices of lithium and
beryllium behave approximately like scandium and titanium lattices.
Therefore I doubted the absolute correctness of the table of elements and developed amendments.
Therefore I doubted the absolute correctness of the table of elements and developed amendments.
This article sets out the views on the classification of all known
chemical elements, those fundamental components of which the Earth and
the entire Universe consists.
The innovation of this work is that in the table of elements constructed according to the Mendeleyev’s law and Van-den- Broek’s rule, new chemical elements with atomic numbers 72-75 and 108-111 are supposedly revealed, and also it is shown that for heavy elements starting with hafnium, the nuclei of atoms contain a larger number of protons than is generally accepted. Perhaps the mathematical apparatus of quantum mechanics missed some solutions because the atomic nucleus in calculations is taken as a point.
All cells in the table are full. If this table takes place, I would like to name groups of elements with the numbers 72-75 and 108-111, the islets of Filipenka Henadzi.
The rule of van den Broeck, a lover of nuclear physics, turned out to be more general than Mendeleyev's periodicity and calculations of quantum mechanics. The table must be filled in all cells according to the law or rule, and if somebody does not fill in, there should be an explanation of this by this law or rule. Therefore, the cells of the physical table were filled in both at http://tableelements.blogspot.com and unknown items with numbers 72-75 and 108-111 appeared. Which required explanation. When considering the results of measuring the charges of nuclei or atomic numbers by James Chadwick, I noticed that the charge of the core of platinum is rather equal not to 78, but to 82, which corresponds to the developed table. For almost 30 years I have raised the question of the repetition of measurements of the charges of atomic nuclei, since uranium is probably more charged than accepted, and it is used at nuclear power plants.
The innovation of this work is that in the table of elements constructed according to the Mendeleyev’s law and Van-den- Broek’s rule, new chemical elements with atomic numbers 72-75 and 108-111 are supposedly revealed, and also it is shown that for heavy elements starting with hafnium, the nuclei of atoms contain a larger number of protons than is generally accepted. Perhaps the mathematical apparatus of quantum mechanics missed some solutions because the atomic nucleus in calculations is taken as a point.
All cells in the table are full. If this table takes place, I would like to name groups of elements with the numbers 72-75 and 108-111, the islets of Filipenka Henadzi.
The rule of van den Broeck, a lover of nuclear physics, turned out to be more general than Mendeleyev's periodicity and calculations of quantum mechanics. The table must be filled in all cells according to the law or rule, and if somebody does not fill in, there should be an explanation of this by this law or rule. Therefore, the cells of the physical table were filled in both at http://tableelements.blogspot.com and unknown items with numbers 72-75 and 108-111 appeared. Which required explanation. When considering the results of measuring the charges of nuclei or atomic numbers by James Chadwick, I noticed that the charge of the core of platinum is rather equal not to 78, but to 82, which corresponds to the developed table. For almost 30 years I have raised the question of the repetition of measurements of the charges of atomic nuclei, since uranium is probably more charged than accepted, and it is used at nuclear power plants.
таблица элементов
| H 1 | He 2 | Li 3 | Be 4 | B 5 | C 6 | N 7 | O 8 | F 9 | Ne 10 | Na 11 | Mg 12 | Al 13 | Si 14 | P1 5 | S 16 | Cl 17 | A 1 | |
| K 19 | Ca 20 | Sc 21 | Ti 22 | V 23 | Cr 24 | Mn 25 | Fe 26 | Co 27 | Ni 28 | Cu 29 | Zn 30 | Ga 31 | Ge 32 | As 33 | Se 34 | Br 35 | Kr 36 | |
| Rb 37 | Sr 38 | Y 39 | Zr 40 | Nb 41 | Mo 42 | Tc 43 | Ru 44 | Rh 45 | Pd 46 | Ag 47 | Cd 48 | In 49 | Sn 50 | Sb 51 | Te 52 | I 53 | Xe 54 | |
| Cs 55 | Ba 56 | La 57 | Ce 58 | Pr 59 | Nd 60 | Pm 61 | Sm 62 | Eu 63 | Gd 64 | Tb 65 | Dy 66 | Ho 67 | Er 68 | Tu 69 | Yb 70 | Lu 71 | ? 72 | |
| ? 73 | ? 74 | ? 75 | Hf 76 | Ta 77 | W 78 | Re 79 | Os 80 | Ir 81 | Pt 82 | Au 83 | Hg 84 | Tl 85 | Pb 86 | Bi 87 | Po 88 | At 89 | Rn 90 | |
| Fr 91 | Ra 92 | Ac 93 | Th 94 | Pa 95 | U 96 | Np 97 | Pu 98 | Am 99 | Cm 100 | Bk 101 | Cf 102 | Es 103 | Fm 104 | Md 105 | No 106 | Lr 107 | ||
Our philosophy that it is impossible to describe nature mathematically by one hundred percent was confirmed. But it strives, of course, to such a description is necessary.
Henadzi Filipenka
Henadzi Filipenka
Each subsequent chemical element is different
from the previous one in that in its core the number of protons
increases by one, and the number of neutrons increases, in
in general, several. In the literature this strange
ratio of the number of neutrons to the number of protons for any
the kernel is not explained. The article proposes a model nucleus,
explaining this phenomenon.
from the previous one in that in its core the number of protons
increases by one, and the number of neutrons increases, in
in general, several. In the literature this strange
ratio of the number of neutrons to the number of protons for any
the kernel is not explained. The article proposes a model nucleus,
explaining this phenomenon.
For the construction of the atomic nucleus model, we note that with alpha-
radioactivity of the helium nucleus is approximately equal to the energy.
Therefore, on the outer layer of the core shell, we place all the protons with such
the same number of neutrons. At the same time, on one energy
Only bosons can be in the
outer shell of the alpha-particle nucleus and are. Inside the Kernel
We will arrange the remaining neutrons, whose task will be
weakening of electrostatic fields of repulsion of protons.
Assuming the core to be spherical, and the radii of the proton and neutron
approximately the same, for any element we get the kernel model,
explaining the ratio of the number of neutrons to the number of protons,
which follows from the packing of the nucleus of the atom by nucleons. Low accuracy for light elements.
radioactivity of the helium nucleus is approximately equal to the energy.
Therefore, on the outer layer of the core shell, we place all the protons with such
the same number of neutrons. At the same time, on one energy
Only bosons can be in the
outer shell of the alpha-particle nucleus and are. Inside the Kernel
We will arrange the remaining neutrons, whose task will be
weakening of electrostatic fields of repulsion of protons.
Assuming the core to be spherical, and the radii of the proton and neutron
approximately the same, for any element we get the kernel model,
explaining the ratio of the number of neutrons to the number of protons,
which follows from the packing of the nucleus of the atom by nucleons. Low accuracy for light elements.
We
construct the table so that to observe the law of Mendeleyev
periodicity, the VanDen-Brook rule and to fill all the cells of the
table. In
quantum mechanics, by default, in each successive element, the charge
of the nucleus increases at its center by one, and the electrons fill
with spdf configurations. Our
nuclear charge is located on the surface, since the number of protons
and the number of neutrons in the nucleus are such that protons and
neutrons should be in the outer layer of the nucleus, and only neutrons
inside, that is, a shell forms on the surface of the nucleus. In addition, protons must be repelled, and also attracted by an electronic fur coat. The question is whether the kernel can be considered a point in the calculations and up to what times? And the question is whether and when the proton will be inside the nucleus. There is also an apparatus of quantum mechanics, which confirmed the law of Mendeleyev. In his calculations, the nucleus and electrons are taken as points.
But if a proton gets into the nucleus for some reason, then the corresponding electron will be on the very "low" orbit. Quantum mechanics still does not notice such electrons. Or in other words, in elements 72-75 and 108-111, some protons begin to be placed inside the nucleus and the charge of the nucleus is screened, in calculations it can not be taken as a point.
I understood this when I thought of Chadwick's experiments on the determination of nuclear charges in particular platinum. If we plot the results from copper through silver to platinum, we see a clear trend on the charge of platinum not 78, but more. I have 82.
This is the correct and real table, not the pieces. Beginning with Hafnium, the number of protons and, correspondingly, neutrons in the nuclei of the elements changes in comparison with what is generally accepted today.
But if a proton gets into the nucleus for some reason, then the corresponding electron will be on the very "low" orbit. Quantum mechanics still does not notice such electrons. Or in other words, in elements 72-75 and 108-111, some protons begin to be placed inside the nucleus and the charge of the nucleus is screened, in calculations it can not be taken as a point.
I understood this when I thought of Chadwick's experiments on the determination of nuclear charges in particular platinum. If we plot the results from copper through silver to platinum, we see a clear trend on the charge of platinum not 78, but more. I have 82.
This is the correct and real table, not the pieces. Beginning with Hafnium, the number of protons and, correspondingly, neutrons in the nuclei of the elements changes in comparison with what is generally accepted today.
Literature:
1) Solid state physics. N.W. Ashcroft, N.D. Mermin. Cornell University, 1975
2) Characteristics of elements. G.V. Samsonov. Moscow, 1976
3) Grundzuge der Anorganischen Kristallchemie. Von. Dr. Heinz Krebs. Universitat Stuttgart, 1968
4) Physics of metals. Y.G. Dorfman, I.K. Kikoin. Leningrad, 1933
5) What affects crystals characteristics. G.G.Skidelsky. Engineer N 8, 1989
1) Solid state physics. N.W. Ashcroft, N.D. Mermin. Cornell University, 1975
2) Characteristics of elements. G.V. Samsonov. Moscow, 1976
3) Grundzuge der Anorganischen Kristallchemie. Von. Dr. Heinz Krebs. Universitat Stuttgart, 1968
4) Physics of metals. Y.G. Dorfman, I.K. Kikoin. Leningrad, 1933
5) What affects crystals characteristics. G.G.Skidelsky. Engineer N 8, 1989
6. Г. Г. Филипенко. «Подозрительные» области в
периодической системе, "Техника и наука", №4,
Москва, 1990.
7. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", №4, Москва, 1991.
периодической системе, "Техника и наука", №4,
Москва, 1990.
7. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", №4, Москва, 1991.
Ключевые слова: atom, neutron, proton, electron, metals, elements, table of elements

Работал над этой проблемой изменения кристаллических структур в зависимости от условий с 3го курса института. В интернете начал размещать на сайтах:
ОтветитьУдалитьhttp://structurecrystal.blogspot.com
http://physicaltable.blogspot.com
А Вы со мною свяжитесь.. я Вам всё укажу и предложу. Автор МД АФС на миллионы лет. Композитор. Совсем другой ум. Геннадий ... уважаемый.
Удалитьin English http://natureofcrystalstructure.blogspot.com
ОтветитьУдалитьhttp://tableelements.blogspot.com
http://nauka-sn.ru/filestore/3(7)2018/FilipenkaH.R.pdf
ОтветитьУдалитьNature of chemical elements.
Let's look at the trends following from this work. The first is the periodicity of the crystal, which is determined not only by the charge of the nucleus and the lattice constant, but also by the charges of the external electrons of the cores of the atom (ions) and with a higher frequency than for the lattice constant. The second relates to direct and inverse gratings, which are used in calculations in the space of wave vectors. Due to the fact that the elementary face-centered crystal lattice is presumably not defined correctly. It was shown that a centrally selected atom interacts with 9 out of 12 neighboring lattice atoms.
УдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьГоворят, что на распределение электронов по энергетическим уровням в твердых телах влияет внутреннее периодическое электрическое поле ионов кристаллической решетки. Сделаем грубый расчет влияния на электрон в зоне проводимости заряда ядра атома (иона) и электрона атомного остова на внешней оболочке иона. Пусть расстояние между атомами равно 4 ангстремам, а между внешним электроном остова и электроном проводимости 0,25 ангстрема, тогда и находим элемент с атомным номером 64, заряд ядра которого воздействует на электрон проводимости с той же силой, что и внешний электрон остова. Гадолиний. Отсюда видим, что влияние на электрон проводимости и иона и электрона на внешней оболочке атомного остова примерно одинаковы!!! Грубо конечно, тем не менее зонную теорию нужно пересмотреть по причине более частого периодического поля.
ОтветитьУдалитьОчень интересные наблюдения, хотел добавить свой "пазл" в Вашу работу, (новая теория ЭДС) в ютубе,
УдалитьКратко говоря наблюдая за нейтралью электрогенератора постоянного тока очевидно, что энергия идет с нейтральной точки соединения звездой, это как пример, если нейтраль убрать из зоны влияния магнитных полей ,то амперметрр все равно показывает прохождения тока от нейтральной точки к катушкам статора. Если эту нейтраль установить в вакууме камеру то медная кристаллическая решетка превратится в элемент на порядок ниже по таблице елемеетов
УдалитьIt is said that the internal periodic electric field of the ions of the crystal lattice affects the distribution of electrons over the energy levels in solids. We make a rough calculation of the effect on the electron in the conduction band of the charge of the nucleus of the atom (ion) and the electron of the atomic core on the outer shell of the ion. Let the distance between atoms be 4 angstroms, and between the outer electron of the core and the conduction electron 0.25 angstrom, then we find an element with atomic number 64 whose charge of the nucleus affects the conduction electron with the same force as the outer electron of the core. Gadolinium. Hence we see that the effect on the conduction electron and the ion and the electron on the outer shell of the atomic core is approximately the same !!! Roughly, of course, nevertheless the band theory needs to be revised because of the more frequent periodic field.
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитья это спросил, чтобы понять вы мне про единичный атом урана и его распад именно на барий и криптон при каких то определенных условиях с гарантией сообщаете или статистику так называемой золы приводите... уверен что условий для именно такого распада не знаете, а просто даете статистику разных осколков выведенных из того что известен был уран92 и только... из урана96 можно вывести тот же барий и цирконий или лантан и иттрий, которые лежат ближе к максимумам кривой, чем барий и криптон или лантан и бром... та же зола но более соответствующая кривой распределения осколков с тем же химическим составом... НА ЭТИХ ПРИМЕРАХ Я УБЕДИЛСЯ В ПРАВИЛЬНОСТИ ЗАРЯДА ЯДРА АТОМА УРАНА96
ОтветитьУдалитьИз обсуждения на Химик.ру
УдалитьDear, you explain to me how and under what conditions the atom 92 of uranium decays into barium and krypton and how it is registered. I asked this in order to understand to me about a single uranium atom and its decomposition into barium and krypton under certain specific conditions with a guarantee or you give the statistics of the so-called ash ... I am sure that you don’t know the conditions for such decay, but simply give the statistics of different fragments derived from what was known was uranium 92 and only ... from uranium96 you can derive the same barium and zirconium or lanthanum and yttrium, which lie closer to the curve maxima than barium and krypton or lanthanum and bromine ... the same ash but more appropriate curve the distribution of splinters with the same chemical composition ... ON THESE EXAMPLES I HAVE BEEN ASSESSED OF THE URANIUM NUCLEAR CHARGE OF 96
ОтветитьУдалитьDo you know at least one scientist who counted or experimentally determined the number of protons in the nuclei of the hafnium atom and the elements following it?
ОтветитьУдалитьWho will check the atomic numbers of the chemical elements following hafnium?
Этот комментарий был удален автором.
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьI prefer Poster presentation
ОтветитьУдалитьNature of chemical elements
Henadzi Filipenka
Independent researcher, Grodno, Belarus
E-mail: hfilipenk@gmail.com
Nature of chemical elements. Henadzi Filipenka. 6a-7 Boldina str. Grodno 230030 Belarus.
Abstract
The main problem is that using X-ray to determine the crystal lattices of different materials, and why they are such and not others is not yet known. For example, copper crystallizes in the fcc lattice, and iron in the bcc, which upon heating becomes fcc and this transition is used in the heat treatment of steels.
The literature cites many factors affecting the crystallization of atoms, so I decided to remove them as much as possible, and the metal model in the article, let’s say, ideal, i.e. all atoms are the same (pure metal) without inclusions, without implants, without defects, etc., using the Hall effect and other data on the properties of the elements, as well as Ashcroft and Mermin's calculations - the main determining factor for the type of lattice was the external electrons of the atom’s core or ion that turned into as a result of the transfer of part of the electrons of the atom to the conduction band of the crystal.
It turned out that the metal bond is caused not only by the socialization of electrons, but also by the external electrons of the atomic cores, which determine directivity or type of crystal lattice.
A change in the type of metal lattice can be associated with the transition of an electron into the conduction band or its return from this band.
http://nauka-sn.ru/filestore/3(7)2018/FilipenkaH.R.pdf
Keywords
Chemical elements, table of elements, electron, proton, neutron, crystal structure
Biography
Born in 1948 in the Grodno region of the Belarusian SSR of the Soviet Union. After serving in the army, he graduated from the Leningrad Electrotechnical Institute (LETI) with a degree in semiconductors and dielectrics.
Single crystals of yttrium garnet were grown in lead oxide melts at NPO Ferrit. Since 1986, he worked out the technology of production of products by powder metallurgy methods at the Kazan Scientific Research Radiotechnological Institute. He graduated from labor as a teacher of materials science at the Grodno Electrotechnical College in 2014.
During his studies at LETI, he tried to explain the nature of phase transitions in barium titanate. During his career, he sought the mechanisms of interaction of atoms during the formation of various crystal lattices of metals. Along the way, I built a table of elements.
I live in the city of Grodno, Belarus. Wife, daughter, cat.
Presenting Author Details and Photo
Full name: Henadzi Filipenka
Email ID: hfilipenk@gmail.com
Phone No: +375295888451
Этот комментарий был удален автором.
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьСамый простой, известный на сегодняшний день, состоящий из 9 вершин, 17 рёбер и 14 граней, будет сейчас построен. Его в 1978 году придумал немецкий математик Клаус Штеффен.
ОтветитьУдалитьРазвёртка многогранника Штеффена состоит из двух одинаковых частей и «крышки». Даже помня внешний вид развёртки, но не зная длин рёбер, построить такой многогранник самому сложно: возможность изгибаться — это всё же исключение для многогранников, и таких относительно мало.
Можно показать, что несамопересекающийся многогранник с 7 и меньшим числом вершин изгибаться не может. Описанный изгибаемый многогранник Штеффена имеет 9 вершин.
Читать полностью: http://www.etudes.ru/ru/etudes/polyhedra-flexible
© 2002—2019, Математические этюды
Посмотрим на тренды следующие из этой работы. Первое, это периодичность кристалла, которая определяется не только зарядом ядра и постоянной решетки, а и зарядами внешних электронов остовов атома (ионов) и с большей частотой, чем для постоянной решетки. Второе относится к прямым и обратным решеткам, которые используются при расчетах в пространстве волновых векторов. По причине того, что элементарная гранецентрированная кристаллическая решетка предположительно определена не правильно. В работе показано, что центрально избранный атом взаимодействует с 9 из 12 соседних атомов решетки.
УдалитьПосмотрим на тренды следующие из этой работы. Первое, это периодичность кристалла, которая определяется не только зарядом ядра и постоянной решетки, а и зарядами внешних электронов остовов атома (ионов) и с большей частотой, чем для постоянной решетки. Второе относится к прямым и обратным решеткам, которые используются при расчетах в пространстве волновых векторов. По причине того, что элементарная гранецентрированная кристаллическая решетка предположительно определена не правильно, все квантовомеханические расчеты в твердых тела подлежат пересмотру. В работе показано, что центрально избранный атом взаимодействует с 9 из 12 соседних атомов решетки.
Удалитьhttp://www.etudes.ru/data/etudes/polyhedra-flexible/10.jpg
ОтветитьУдалитьВ 2019 году этой таблице исполнилось 30 лет. Кто докажет ее ошибочность?
ОтветитьУдалитьЭтот комментарий был удален автором.
ОтветитьУдалитьLet's look at the trends following from this work. The first is the periodicity of the crystal, which is determined not only by the charge of the nucleus and the lattice constant, but also by the charges of the external electrons of the cores of the atom (ions) and with a higher frequency than for the lattice constant. The second relates to direct and inverse gratings, which are used in calculations in the space of wave vectors. Due to the fact that the elementary face-centered crystal lattice is presumably not defined correctly. It was shown that a centrally selected atom interacts with 9 out of 12 neighboring lattice atoms.
ОтветитьУдалитьПосмотрим на тренды следующие из этой работы. Первое, это периодичность кристалла, которая определяется не только зарядом ядра и постоянной решетки, а и зарядами внешних электронов остовов атома (ионов) и с большей частотой, чем для постоянной решетки. Второе относится к прямым и обратным решеткам, которые используются при расчетах в пространстве волновых векторов. По причине того, что элементарная гранецентрированная кристаллическая решетка предположительно определена не правильно. В работе показано, что центрально избранный атом взаимодействует с 9 из 12 соседних атомов решетки.
K зонной теории твердого тела, to the zone theory of solids
ОтветитьУдалить==============================================================================
Углублено понятие металлической связи, определены факторы способствующие образованию определенного типа кристаллических решеток, построена модель ядра атома, обьясняющая количества нейтронов для ядер химических элементов, скорректирована таблица элементов. Элементарная ячейка ГЦК решетки предположительно образована 9 атомами в первом координационном числе и наверное 6 атомами во втором координационном числе в отличие от современно принятого: 12 в первом и 6 во втором.
The concept of metal bonds is deepened, factors contributing to the formation of a certain type of crystal lattices are determined, a model of the atomic nucleus is constructed that explains the number of neutrons for the nuclei of chemical elements, the table of elements is adjusted. The unit cell of the fcc lattice is supposedly formed by 9 atoms in the first coordination number and probably 6 atoms in the second coordination number, unlike the modern one: 12 in the first and 6 in the second.
Начал сомневаться 9 и 6 или 12 и 3- вроде как первое компактней...
УдалитьI began to doubt 9 and 6 or 12 and 3 - it seems like the first is more compact ...
Электронная конфигурация атома меди в основном состоянии записывается виде 1s22s22p63s23p63d104s1 вместо предполагаемой формулы 1s22s22p63s23p63d94s2. Но не в этом дело. Попытаемся найти причину образования кристаллической решетки типа ГЦК для меди и никеля. И у меди, и у никеля атом окружен 12 подобными в первом координационном числе и 6 во втором. Казалось бы бери из оболочки 18 последних электронов для связи атомов и получай ГЦК. Но и у меди и у никеля кроме электронов связи есть электроны проводимости. Значит электронов связи меньше 18 и их достаточно для образования ГЦК. У железа 14 электронов связи (8+6) и они формируют ОЦК. Плотность ОЦК- 68%, а ГЦК-74%. Отсюда я делаю вывод, что у меди и никеля по 15 электронов связи. Но (12+3) или (9+6) должна показать экспериментальная проверка.
УдалитьWhat do I think of the valency of metal atoms in their ideal single crystals consisting of only identical atoms?
ОтветитьУдалитьthe valency in metals is different, for example, for cesium-8,
potassium-8, and magnesium and aluminum-9, iron and chromium-14, copper, gold and platinum-15 ...
Что я думаю о валентности атомов металлов в их идеальных монокристаллах, состоящих только из одинаковых атомов?
получается, что... валентность в металлах разная например у цезия-8
у калия-8, а у магния и алюминия-9, у железа и хрома-14, у меди золота и платины-15...
in order to explain the nature of the mechanical properties of solids, something must be presented as a crystal ... but a lone atom is certainly not a crystal and it is not easy to take it for testing ... atomic cores (ions) become crystals after their crystallization (atoms) ... hardness fragility plasticity is ensured by external valence bond electrons of these atomic cores ...
Удалитьчтобы обьяснить природу механических свойств твердых тел необходимо что-то представить как кристалл... но одинокий атом конечно не кристалл и взять его для испытаний не просто... кристаллами становятся атомные остовы (ионы) после их (атомов) кристаллизации... твердость хрупкость пластичность обеспечивают внешние валентные электроны связи этих атомных остовов...
So the valence of the iron atom is 14 in a single crystal of iron, and the valence of a copper atom is 15 in a single crystal of copper, hence the mechanical properties. Potassium, sodium have 8 bond electrons, aluminum and magnesium have 9. Valence in single crystals of these pure metals. Bond electrons are located closer to conduction electrons than charged nuclei of atoms (ions); therefore, it is necessary to take into account the periodicity in crystals not only associated with nuclei, but also with bond electrons. Since the fcc crystal lattice has supposedly changed, its application in the theory of wave vectors during transitions from the forward lattice to the reciprocal lattice is subject to discussion.
УдалитьИтак валентность атома железа равна 14 в монокристалле железа, а атома меди 15 в монокристалле меди, отсюда и механические свойства. У калия, натрия по 8 электронов связи, у алюминия и магния по 9. Валентность в монокристаллах этих чистых металлов. Электроны связи расположены ближе к электронам проводимости, чем заряженные ядра атомов (ионов), поэтому необходимо учитывать периодичность в кристаллах не только связанную с ядрами, но и с электронами связи. Так как предположительно изменилась кристаллическая решетка ГЦК, ее применение в теории волновых векторов при переходах прямая решетка в обратную решетку подлежит обсуждению.
The electronic configuration of the copper atom in the ground state is written in the form 1s22s22p63s23p63d104s1 instead of the assumed formula 1s22s22p63s23p63d94s2. But that's not the point. Let us try to find the reason for the formation of a crystal lattice of the fcc type for copper and nickel. In both copper and nickel, the atom is surrounded by 12 similar ones in the first coordination number and 6 in the second. It would seem that you take the last 18 electrons from the shell to bond the atoms and get fcc. But copper and nickel, in addition to bond electrons, have conduction electrons. This means that there are less than 18 bond electrons and there are enough of them for the formation of fcc. Iron has 14 bond electrons (8 + 6) and they form bcc. The density of the bcc is 68%, and the fcc is 74%. From this I conclude that copper and nickel each have 15 bond electrons. But (12 + 3) or (9 + 6) should be shown by experimental verification.
УдалитьDear Sirs!
ОтветитьУдалитьI give some explanations to my work. The atomic nucleus model was developed in order to clarify the adjusted table of elements. Between lutetium and hafnium, the difference in atomic masses does not reach four units, while new elements with atomic numbers 72-75 are placed there. How can nucleons be packed in a nucleus so that it is drip and shell and with the necessary number of neutrons? Such a nucleus is obtained if alpha particles are placed in the surface layer, and only neutrons are inside the nucleus. In this case, in new chemical elements with numbers 72-75 inside the nucleus, the neutron can be replaced by a proton, and therefore the atomic mass of the elements between lutetium and hafnium will vary slightly. The model was obtained by considering the structure of the nuclei of atoms from heavy to light.
Sir Chadwick probably made a mistake after all, measuring the charge of the platinum core, which is obviously 82, according to the constructed table of elements.
The main achievement of my work is the fact that the present first coordination number for atoms in single crystals of pure metals (fcc and HEC crystal lattices) was determined to be 9. This number is derived from the physical and chemical properties of crystals and is not related to beautiful symmetrical pictures.
What do I think of the valency of metal atoms in their ideal single crystals consisting of only identical atoms?
it turns out that ... the valency in metals is different, for example, for cesium-8, for potassium-8, and for magnesium and aluminum-9, for iron and chromium-14, for copper, gold and platinum-15 ...
Special thanks to such scientists as Ganzhorn and Delinger, Ashcroft and Mermin, as well as to Professor Boris Filippovich Ormont, from whom I studied crystal chemistry.
Sincerely Henadzi Filipenka
Уважаемые господа! Привожу некоторые пояснения к моей работе. Модель ядра атома была разработана для того, чтобы пояснить скорректированную таблицу элементов. Между лютецием и гафнием разница в атомных массах не достигает четырех единиц, в то время как там размещаются новые элементы с атомными номерами 72-75. Как можно упаковать нуклоны в ядре чтобы оно было капельным и оболочечным и с нужным количеством нейтронов? Таким ядро получается, если в поверхностном слое разместить альфа-частицы, а внутри ядра только нейтроны. В этом случае у новых химических элементов с номерами 72-75 внутри ядра нейтрон может замещаться протоном и поэтому атомная масса элементов между лютецием и гафнием будет изменяться незначительно. Модель была получена при рассмотрении структур ядер атомов от тяжелых к легким.
ОтветитьУдалитьСэр Чедвик, наверное, все таки ошибся, измеряя заряд ядра платины, который очевидно равен 82, согласно построенной таблицы элементов.
Основным достижением моей работы считаю то, что было определено настоящее первое координационное число для атомов в монокристаллах чистых металлов (ГЦК и ГЕК кристаллических решеток) равное 9. Число это выведено из физических и химических свойств кристаллов и не имеет отношния к красивым симметричным картинкам.
Что я думаю о валентности атомов металлов в их идеальных монокристаллах, состоящих только из одинаковых атомов?
получается, что... валентность в металлах разная например у цезия-8,у калия-8, а у магния и алюминия-9, у железа и хрома-14, у меди золота и платины-15...
Особая благодарность таким ученым как Ганцхорн и Делингер, Ашкрофт и Мермин, а также профессору Борису Филипповичу Ормонту, у которого я изучал кристаллохимию.
if the nucleus is large and the electron is small, which is probably correct, then the electron will never fall on the nucleus because when approaching on the side of the electron looking at the nucleus, fewer and fewer lines of force working on attraction will end, and on the opposite side of the electron will be closed more and more repulsive power lines ...
ОтветитьУдалитьthe electron will be near some equilibrium position ... for a single hydrogen atom, you can probably talk about the orbit because the only one electron there
Этот комментарий был удален автором.
ОтветитьУдалитьLet us try to suggest the nature of ferromagnetism from our reasoning. From the electronic configurations of the atoms of iron, cobalt and nickel, we see that
ОтветитьУдалить26 Fe iron 1s2 2s2 2p6 3s2 3p6 4s2 3d6
27 Co cobalt 1s2 2s2 2p6 3s2 3p6 4s2 3d7
28 Ni Nickel 1s2 2s2 2p6 3s2 3p6 4s2 3d8
After crystallization of atoms in a solid, the skeleton of an atom can be oriented with respect to two electrons from 3s2. Which probably allows you to respond to an external magnetic field by rotating the core, as on the axis, and thereby significantly increase the value of this external field.
In most materials, domains are microscopic in size, on the order of 10-4 - 10-6 m.
Удалитьapproximately equal to grains or crystallites in the structure of polycrystalline metals and alloys
Попытаемся предположить из наших рассуждений природу ферромагнетизма. Из электронных конфигураций атомов железа, кобальта и никеля видим, что
ОтветитьУдалить26 Fe железо 1s2 2s2 2p6 3s2 3p6 4s2 3d6
27 Co кобальт 1s2 2s2 2p6 3s2 3p6 4s2 3d7
28 Ni никель 1s2 2s2 2p6 3s2 3p6 4s2 3d8
после кристаллизации атомов в твердое тело остов атома может ориентироваться относительно двух электронов из 3s2. Что наверное позволяет реагировать на внешнее магнитное поле вращением остова, как на оси, и тем самым значительно повышать величину этого внешнего поля.
В большинстве материалов домены имеют микроскопические размеры, порядка 10-4 - 10-6 м.
Удалитьпримерно равны зернам или кристаллитам в структуре поликристаллических металлов и сплавов
Будет ли когда-нибудь проверен эксперимент сэра Чедвика по измерению заряда ядра атома платины?
ОтветитьУдалитьWill Sir Chadwick's experiment on measuring the platinum core charge ever be tested?
“Benjamin Briel Lee was very professional at all times, keeping me aware of everything that was happening, If I had any questions he was always available to answer. This was my first home purchase, I didn’t know much about the loan process, he made it very easy to understand the things I had questions about. I really enjoyed working with him.”
ОтветитьУдалитьHe's a loan officer working with a group of investor's who are willing to fund any project or loan you any amount with a very low interest.Contact Benjamin Briel Lee E-Mail: lfdsloans@outlook.com Whats-App Number: +1-989-394-3740.
Dear Maria Hugo thank you very much!
УдалитьSincerely Henadzi Filipenka
A connection was found between the external electrons of atoms and the type of crystal lattices.
ОтветитьУдалитьНайдена связь между внешними электронами атомов и типом кристаллических решеток.
ОтветитьУдалитьРасширенная и углубленная теория металлической связи.
Основная проблема состоит в том, что используя рентген определили типы кристаллических решеток разных металлов,а почему они такие, а не другие пока не известно. Например медь кристаллизуется в ГЦК решетку, а железо в ОЦК, которая при нагреве становиться ГЦК и этот переход используется при термообработке сталей.
Обычно в литературе металлическая связь описывается, как осуществленная посредством обобществления внешних электронов атомов и не обладающая свойством направленности. Хотя встречаются попытки (см. ниже) объяснения направленной металлической связи т.к. элементы кристаллизуются в определенный тип решетки. Основные типы кристаллических решеток металлов объемно-центрированная кубическая; гранецентрированная кубическая; гексагональная плотноупакованная.
Пока невозможно в общем случае вывести из квантовомеханических расчетов кристаллическую структуру металла по электронному строению атома, хотя, например, Ганцхорн и Делингер указали на возможную связь между наличием кубической объемно-центрированной решетки в подгруппах титана, ванадия, хрома и наличием в атомах этих металлов валентных d-орбиталей.
Нетрудно заметить, что четыре гибридные орбитали направлены по четырем телесным диагоналям куба и хорошо приспособлены для связи каждого атома с его 8 соседями в кубической объемноцентрированной решетке. При этом оставшиеся орбитали направлены к центрам граней элементарной ячейки и, возможно, могут принимать участие в связи атома с шестью его вторыми соседями. Первое координационное число (К.Ч.1) \"8\"плюс второе координационное число (К.Ч.2) \"6\" в сумме равно \"14\".
Покажем, что металлическая связь в плотнейших упаковках (ГЕК и ГЦК) между центральноизбранным атомом и его соседями в общем случае, предположительно, осуществляется посредством 9 (девяти) направленных связей, в отличие от числа соседей равного 12 (двенадцати) (координационное число).
В литературе приводится много факторов влияющих на кристаллизацию поэтому решил их максимально убрать, и модель металла в статье скажем так ,идеальная, т.е. все атомы одинаковые (чистый металл), кристаллические решетки без включений, без внедрений, без дефектов и т.д. Используя эффект Холла и другие данные по свойствам, а также рассчеты Ашкрофта и Мермина , у меня главным определяющим тип решетки фактором, оказались внешние электроны остова атома или иона, который получился в результате передачи части электронов в зону проводимости.
Оказалось, что металлическая связь обусловлена не только обобществлением электронов, а и внешними электронами атомных остовов, которые определяют направленность или тип кристаллической решетки.
Попытаемся связать внешние электроны атома данного элемента со структурой его кристаллической решетки, учитывая необходимость направленных связей (химия) и наличие обобществленных электронов (физика), ответственных за гальваномагнитные свойства.
основную часть работы смотрите на стр.
https://natureofchemicalelements.blogspot.com
Основным достижением моей работы считаю то, что было определено настоящее первое координационное число для атомов в монокристаллах чистых металлов (ГЦК и ГЕК кристаллических решеток) равное 9. Число это выведено из физических и химических свойств кристаллов.
Extended and in-depth theory of metallic bonds.
ОтветитьУдалитьThe main problem is that, using X-rays, the types of crystal lattices of different metals were determined, and why they are so and not others is not yet known. For example, copper crystallizes in the fcc lattice, and iron in the bcc lattice, which when heated becomes fcc and this transition is used in heat treatment of steels.
Usually in the literature, the metallic bond is described as carried out through the socialization of the outer electrons of the atoms and does not have the property of directionality. Although there are attempts (see below) to explain the directional metal bond since the elements crystallize into a specific type of lattice. The main types of crystal lattices of metals are body-centered cubic; face-centered cubic; hexagonal close-packed.
It is still impossible in the general case to deduce the crystal structure of a metal from the electronic structure of the atom from quantum-mechanical calculations, although, for example, Ganzhorn and Delinger pointed out a possible connection between the presence of a cubic body-centered lattice in the subgroups of titanium, vanadium, chromium and the presence of valence d in the atoms of these metals -orbitals.
It is easy to see that the four hybrid orbitals are directed along the four solid diagonals of the cube and are well suited for bonding each atom with its 8 neighbors in a body-centered cubic lattice. In this case, the remaining orbitals are directed to the centers of the unit cell faces and, possibly, can take part in the bond of the atom with its six second neighbors. The first coordination number (K.Ch.1) \ "8 \" plus the second coordination number (C.Ch.2) \ "6 \" in total is \ "14 \".
Let us show that the metallic bond in the closest packing (HEC and FCC) between the centrally selected atom and its neighbors, in the general case, is presumably carried out through 9 (nine) directional bonds, in contrast to the number of neighbors equal to 12 (twelve) (coordination number).
In the literature, there are many factors affecting crystallization, so I decided to remove them as much as possible, and the metal model in the article, let's say, is ideal, i.e. all atoms are the same (pure metal), crystal lattices without inclusions, without interstices, without defects, etc. Using the Hall effect and other data on properties, as well as calculations by Ashcroft and Mermin, for me the main factor determining the type of lattice turned out to be the outer electrons of the core of an atom or ion, which resulted from the transfer of some of the electrons to the conduction band.
It turned out that the metallic bond is due not only to the sharing of electrons, but also to the outer electrons of the atomic cores, which determine the direction or type of the crystal lattice.
Let's try to connect the outer electrons of an atom of a given element with the structure of its crystal lattice, taking into account the need for directed bonds (chemistry) and the presence of socialized electrons (physics) responsible for galvanomagnetic properties.
see the main part of the work on p.
https://natureofchemicalelements.blogspot.com in Russian and in English with comments
I consider the main achievement of my work that the real first coordination number for atoms in single crystals of pure metals (fcc and HEC crystal lattices) was determined equal to 9. This number was deduced from the physical and chemical properties of crystals.
The electronic configuration of the copper atom in the ground state is written in the form 1s22s22p63s23p63d104s1 instead of the assumed formula 1s22s22p63s23p63d94s2. But that's not the point. Let us try to find the reason for the formation of a crystal lattice of the fcc type for copper and nickel. In both copper and nickel, the atom is surrounded by 12 similar ones in the first coordination number and 6 in the second. It would seem that you take the last 18 electrons from the shell to bond the atoms and get fcc. But copper and nickel, in addition to bond electrons, have conduction electrons. This means that there are less than 18 bond electrons and there are enough of them for the formation of fcc. Iron has 14 bond electrons (8 + 6) and they form bcc. The density of the bcc is 68%, and the fcc is 74%. From this I conclude that copper and nickel each have 15 bond electrons. But (12 + 3) or (9 + 6) should be shown by experimental verification.
Удалить
ОтветитьУдалитьэлементы 72-75 можно поискать здесь-
Таблица изотопов лютеция
Символ
нуклида Z(p) N(n) Масса изотопа[9]
(а. е. м.) Период
полураспада[10]
(T1/2) Спин и чётность
ядра[10]
Энергия возбуждения
150Lu 71 79 149,97323 43 мс 2+
150mLu 34 кэВ 80 мкс 1
151Lu 71 80 150,96758 80,6 мс 11/2-
151mLu 77 кэВ 16 мкс 3/2+
152Lu 71 81 151,96412 650 мс 5-
153Lu 71 82 152,95877 900 мс 11/2-
153m1Lu 80 кэВ 1 с 1/2+
153m2Lu 2,5025 МэВ 100 нс 23/2-
153m3Lu 2,6329 МэВ 15 мкс 27/2-
154Lu 71 83 153,95752 1 с 2-
154m1Lu 58 кэВ 1,12 с 9+
154m2Lu 2,562 МэВ 35 мкс 17+
155Lu 71 84 154,954316 68,6 мс 11/2-
155m1Lu 20 кэВ 138 мс 1/2+
155m2Lu 1,7810 МэВ 2,70 мс 25/2-
156Lu 71 85 155,95303 494 мс 2-
156mLu 220 кэВ 198 мс 9+
157Lu 71 86 156,950098 6,8 с 1/2+
157mLu 21,0 кэВ 4,79 с 11/2-
158Lu 71 87 157,949313 10,6 с 2-
159Lu 71 88 158,94663 12,1 с 1/2+
159mLu 100 кэВ 10 с 11/2-
160Lu 71 89 159,94603 36,1 с 2-
160mLu 0 кэВ 40 с
161Lu 71 90 160,94357 77 с 1/2+
161mLu 166 кэВ 7,3 мс 9/2-
162Lu 71 91 161,94328 1,37 мин 1-
162m1Lu 120 кэВ 1,5 мин 4-
162m2Lu 300 кэВ 1,9 мин
163Lu 71 92 162,94118 3,97 мин 1/2+
164Lu 71 93 163,94134 3,14 мин 1-
165Lu 71 94 164,939407 10,74 мин 1/2+
166Lu 71 95 165,93986 2,65 мин 6-
166m1Lu 34,37 кэВ 1,41 мин 3-
166m2Lu 42,9 кэВ 2,12 мин 0-
167Lu 71 96 166,93827 51,5 мин 7/2+
167mLu 0 кэВ 1 мин 1/2-
168Lu 71 97 167,93874 5,5 мин 6-
.....
items 72-75 can be found here-
ОтветитьУдалитьList of isotopes..... 150Lu 71 79 149.97323(54)# 43(5) ms p (80%) 149Yb (2+)
β+ (20%) 150Yb
150mLu 34(15) keV 80(60) μs
[30(+95−15) μs] p 149Yb (1, 2)
151Lu 71 80 150.96757682 80.6(5) ms p (63.4%) 150Yb (11/2−)
β+ (36.6%) 151Yb
151mLu 77(5) keV 16(1) μs p 150Yb (3/2+)
152Lu 71 81 151.96412(21)# 650(70) ms β+ (85%) 152Yb (5−, 6−)
β+, p (15%) 151Tm
153Lu 71 82 152.95877(22) 0.9(2) s α (70%) 149Tm 11/2−
β+ (30%) 153Yb
153m1Lu 80(5) keV 1# s IT 153Lu 1/2+
153m2Lu 2502.5(4) keV >0.1 μs IT 153Lu 23/2−
153m3Lu 2632.9(5) keV 15(3) μs IT 153m2Lu 27/2−
154Lu 71 83 153.95752(22)# 1# s β+ 154Yb (2−) ....
......
хорошо согласуется с природой сверхпроводимости
ОтветитьУдалитьЭлектроны в зоне проводимости при низких температурах обьединяются в газ Бозе-Эйнштейна, который обладает свойством сверхтекучести, поэтому, так называемая сверхпроводимость на самом деле есть сверхтекучесть электронного газа без сопротивления структуры кристалла.
я пояснил почему сопротивление току есть и при переходе осталось, а электронный газ благодаря сверхтекучести движется по проводнику неограниченно долго... а также и почему этот ток не бесконечно большой при так называемом нулевом сопротивлении сверхпроводника первого рода.
Nature of superconductivity.
ОтветитьУдалитьElectrons in the conduction band at low temperatures are combined into a Bose-Einstein gas, which has the property of superfluidity, therefore, the so-called superconductivity is actually superfluidity of an electron gas without resistance to the crystal structure.
I explained why there is resistance to the current and remained during the transition, and the electron gas, due to superfluidity, moves along the conductor for an infinitely long time ... and also why this current is not infinitely large with the so-called zero resistance of a type I superconductor.
Рассмотрим самый тугоплавкий и самый твердый металл вольфрам. Электронная конфигурация его атома такая [Xe] 4f 14 5d 4 6s 2. Из 20 внешних электронов 14 нужны для связей с соседними атомами, и поскольку постоянная Холла положительная и равна примерно единице, то в зоне проводимости вольфрама 2 электрона. Значит 4 электрона из f или из d остаются связанными с ядром. Но для того чтобы быть самым твердым, вольфраму нужно иметь и много электронов связи (14) и много электронов в зоне проводимости (6) для прочной металлической связи. Поэтому требуется проверка экспериментом.
ОтветитьУдалитьConsider the most refractory and hardest metal, tungsten. The electronic configuration of its atom is [Xe] 4f 14 5d 4 6s 2. Of the 20 outer electrons, 14 are needed for bonds with neighboring atoms, and since the Hall constant is positive and equal to approximately unity, there are 2 electrons in the conduction band of tungsten. This means that 4 electrons from f or from d remain associated with the nucleus. But in order to be the hardest, tungsten needs to have both many bond electrons (14) and many electrons in the conduction band (6) for a strong metallic bond. Therefore, verification by experiment is required.
Слабак с ПК: Геннадий ...попробуйте связаться со мною.. есть предложения. Для Вас или Ваших амбициозных друзей учеников. А я помогу сбыться ВСЕМ Вашим планам и мечтам. Москва, уже чемпион Москвы в 72.. и так будет всегда - МД АФС-совершенство, сэр!
ОтветитьУдалитьЭтот комментарий был удален администратором блога.
ОтветитьУдалитьDOI : doi.org/10.33140/JCERP.03.01.02
ОтветитьУдалитьReview Article
Nature of Chemical Elements
Filipenka Henadzi
Дмитрий Иванович строил таблицу согласно атомного веса, и он был прав, т.к. атомный вес характеризовал элемент полностью, если можно так сказать. В эту характеристику входила неявно и периодичность и заряд ядра. Но кто-то собрал после него лантаноиды в одну строчку и разместил ниже таблицы. А у Менделеева после лантана стоял церий. Сейчас после лантана стоит гафний, а это есть грубая ошибка поскольку согласно атомного веса он, гафний, должен располагаться строчкой ниже. Пропущены элементы 72-75 и 108-111, начиная с гафния изменились заряды ядер. После Менделеева началась эпоха квантовой механики и его периодичность красиво вписалась для многих элементов. Потом оказалось, что главный признак элемента заряд ядра. Перед вами таблица построенная согласно зарядов ядер атомов.
ОтветитьУдалитьДоказана ли абсолютная правильность периодической таблицы Менделеева или она правильна с некоторыми исключениями ?
ОтветитьУдалитьDmitry Ivanovich built a table according to atomic weight, and he was right, because. atomic weight characterized the element completely, so to speak. This characteristic implicitly included both the periodicity and the charge of the nucleus. But someone collected the lanthanides after him in one line and placed them below the table. And Mendeleev had cerium after lanthanum. Now after lanthanum there is hafnium, and this is a gross mistake because, according to the atomic weight, it, hafnium, should be located on the line below. Elements 72-75 and 108-111 are omitted, starting with hafnium, the charges of the nuclei have changed.
ОтветитьУдалитьAfter Mendeleev, the era of quantum mechanics began and its periodicity fit beautifully for many elements. Then it turned out that the main feature of the element is the charge of the nucleus. Before you is a table built according to the charges of the nuclei of atoms.
Has the periodic table of elements been proven to be absolutely correct, or correct with some exceptions?
for example, if we build a table according to the charges of the nuclei of atoms, then we get for the elements following after lutetium the charges of the nuclei increased by 4 units ... 72-75 and 108-111 elements not yet discovered.
Почему электрон не падает на ядро? https://dzen.ru/b/Y-e0XQ9qSTkYuAM7
ОтветитьУдалить